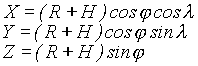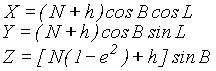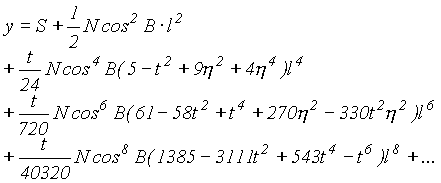Autor
Jacek Lamparski, Instytut Geodezji ART. Olsztyn
© 1998, NAVI sp. z o.o., Wszystkie prawa zastrzeżone.
1. Wstęp
Wkraczająca w coraz więcej dziedzin działalności człowieka technologia satelitarna, wykorzystująca system GPS NAVSTAR powoduje potrzebę zrozumienia relacji między pozycją określoną w układzie satelitarnym a używanym najczęściej na mapie układem współrzędnych.
Zasadnicza różnica pomiędzy tymi układami wynika z tego, że układ satelitarny jest układem trójwymiarowym kartezjańskim (X,Y,Z), a układ stosowany na mapach posiada tylko dwa wymiary płaskie x,y lub krzywoliniowe B i L. Trzecia wielkość - wysokość h punktu wynikająca z rzeźby terenu jest współrzędną "oderwaną" od dwóch pozostałych x i y.
Usystematyzowanie pojęć i relacji pomiędzy układami współrzędnych pozwoli na pełniejsze i efektywniejsze wykorzystanie pozycji, wyznaczonej w układzie satelitarnym.
2. Ogólne zasady realizacji układów
Znane są różne sposoby realizacji układów współrzędnych - wybór sposobu zależy od celu, jakiemu mają służyć.
Każdy układ współrzędnych posiada dokładnie zdefiniowaną charakterystykę geometryczną - położenie początku układu, zdefiniowane kierunki osi współrzędnych lub w przypadku układów krzywoliniowych sposób realizacji kątów określających położenie punktu na określonej powierzchni.
2.1. Układy przestrzenne
Jednym z najstarszych układów współrzędnych jest układ współrzędnych geograficznych. Najlepiej spisywał się na morzu. Położenie punktu opisane jest w nim przy pomocy dwóch kątów określających geocentryczny kierunek do danego punktu.
Punkt może on być położony pod wodą, na powierzchni mórz lub ponad powierzchnią Ziemi - w atmosferze lub w przestrzeni kosmicznej. Ten układ, w którym określone są szerokość geograficzna j i długość geograficzna l jest stosowany do dziś wszędzie tam, gdzie wystarczy niewielka dokładność określenia położenia, rzędu dziesiątek metrów.
Należy zwrócić uwagę na fakt, że oprócz niewielkiej dokładności, w danym układzie nie występuje współrzędna - wysokość punktu, przez którą rozumiemy odstęp punktu od określonej powierzchni odniesienia - geoidy.
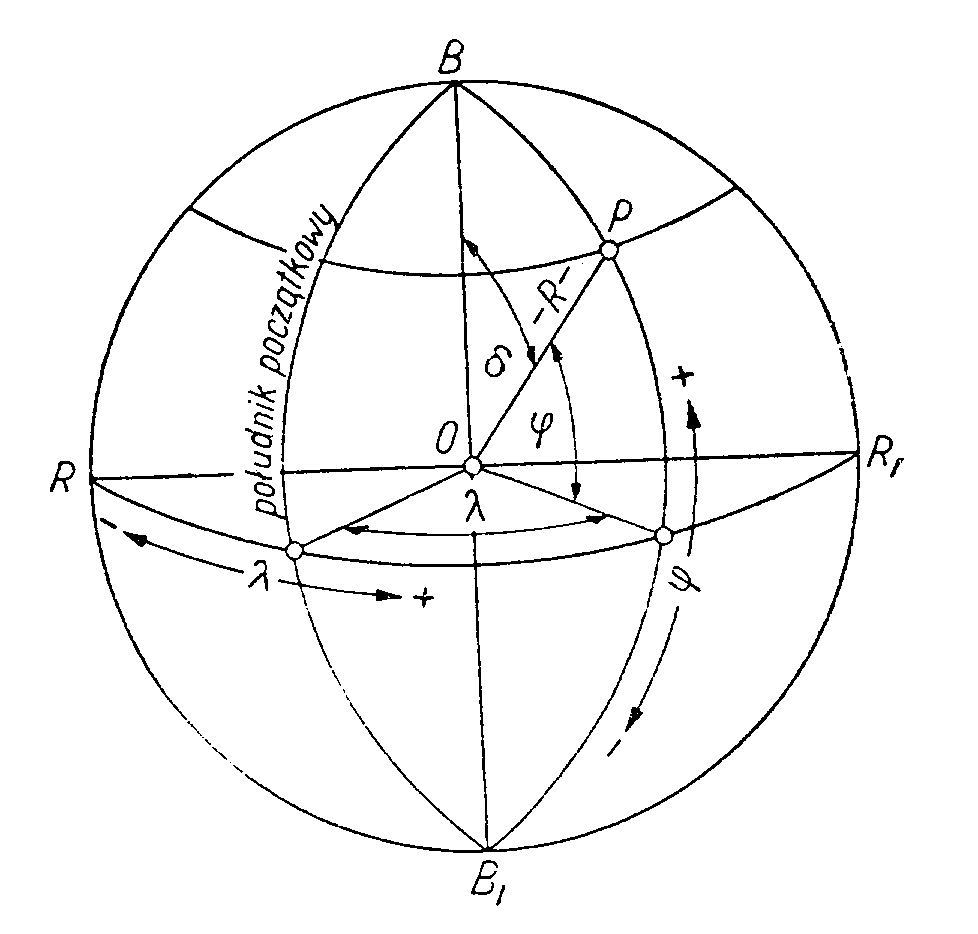
Rys. 1 Układ współrzędnych geograficznych
Wraz z rozwojem nauki i techniki zaczęto dokładniej określać współrzędne. Ponieważ okazało się, że Ziemia nie jest idealnie kulista, wprowadzono układ współrzędnych elipsoidalnych, oparty o elipsoidę obrotową, lepiej pasującą do jej kształtu (rys. 2). Powierzchnią odniesienia jest w tym układzie elipsoida obrotowa.
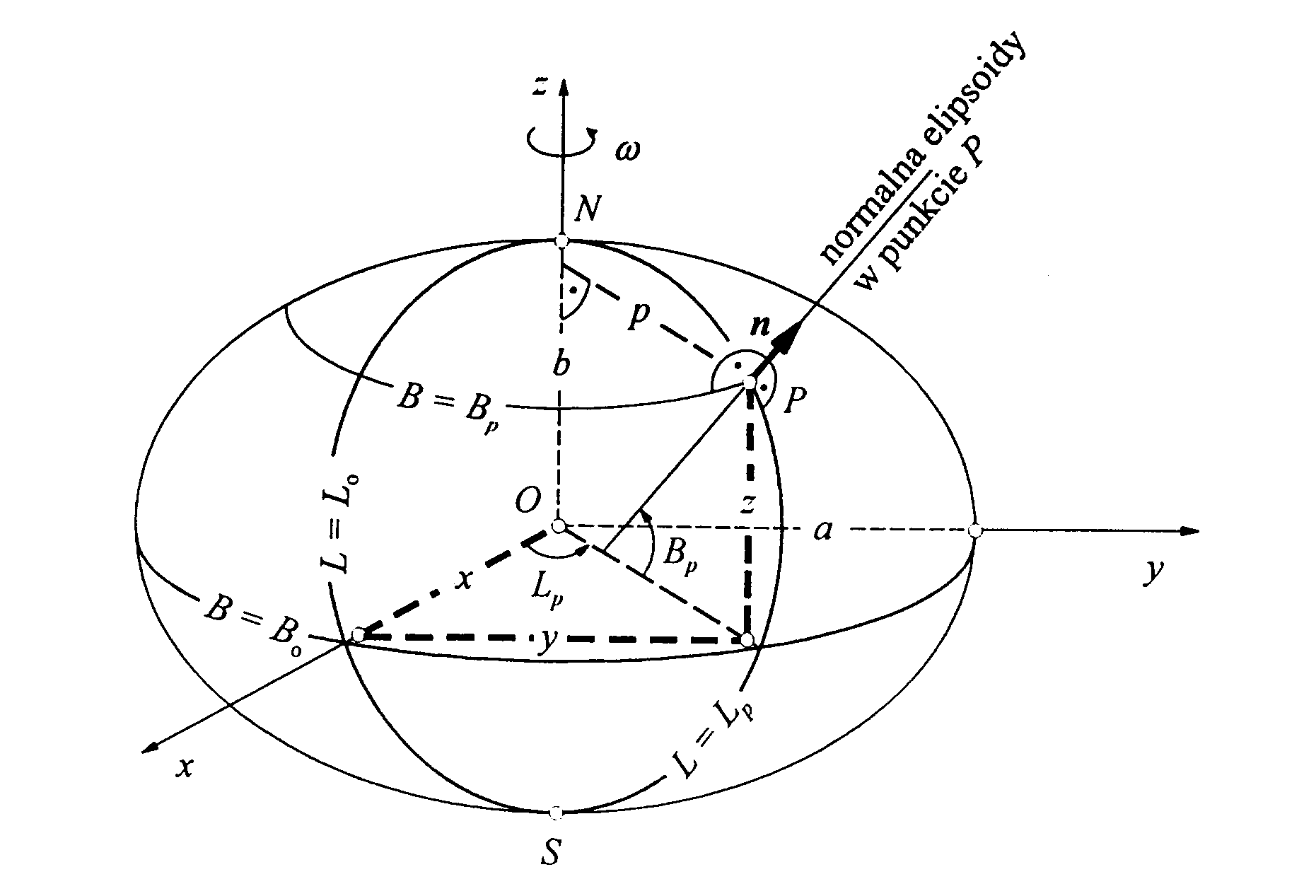
Rys. 2. Układ współrzędnych elipsoidalnych
W układzie współrzędnych elipsoidalnych są określane dokładne współrzędne punktów geodezyjnych. Punkty są zrzutowane z fizycznej powierzchni Ziemi na powierzchnię elipsoidy. Punkt jest określony przy pomocy dwóch współrzędnych - jest to szerokość geodezyjna (elipsoidalna) B oraz długość geodezyjna (elipsoidalna) L. Może być określona również wysokość punktu nad powierzchnią elipsoidy - jest to tzw. wysokość elipsoidalna.
W każdym z tych układów można wpisać układ kartezjański X.Y,Z. Przeliczenie zarówno współrzędnych geograficznych jak i elipsoidalnych na te współrzędne nie stwarza większych trudności (tab. 1).
tab. 1
| Układ geograficzny | Układ elipsoidalny |
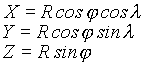 jeżeli punkt jest położony H nad kulą
|
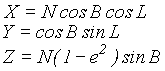 jeżeli punkt jest położony nad elipsoidą
|
Wzory do zamiany odwrotnej są trudniejsze do zrealizowania. W przypadku zastosowania elipsoidy wymagają procedury iteracyjnej (tab.2).
tab. 2
| Układ geograficzny | Układ elipsoidalny |
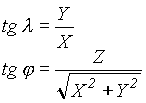 |
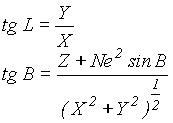 |
Układ WGS84 jest układem globalnym, w którym współrzędne mogą być określone zarówno w układzie kartezjańskim jak i elipsoidalnym. Współrzędne X,Y,Z odnoszą się do elipsoidy WGS84, a więc mogą być przeliczane dokładnie przy pomocy powyższych formuł (w tabeli po prawej stronie).
Na mapach może być naniesiona siatka współrzędnych elipsoidalnych B i L. Nie musi to jednak być elipsoida globalna o początku w środku mas Ziemi - może to być elipsoida przesunięta i obrócona, tak jak np. elipsoida Krasowskiego, używana w Polsce. Niektóre mapy wojskowe używają również siatek współrzędnych odniesionych do systemu WGS84.
2.2. Układy płaskie x,y.
Ponieważ dokładne mapy przedstawiają obraz płaski, wygodniej jest używać siatek współrzędnych prostokątnych x,y, które mogą być zapewnione tylko poprzez odpowiednie odwzorowanie kartograficzne elipsoidy na powierzchnię, dającą rozwinąć się jako płaszczyznę.
Przy konstrukcji różnorodnych map kartografowie używają dziesiątek różnych odwzorowań.
Różnią się one cechami, walorami praktyczności, stopniem komplikacji.
Nie da się przedstawić dokładnie powierzchni kulistej, a tym bardziej elipsoidalnej na płaszczyźnie bez zniekształcenia rzeczywistego obrazu. Pewne warunki mogą być jednak zachowane bez zniekształceń - np. kąty rzeczywiste będą na mapie w odwzorowaniu takie same. Mamy wówczas odwzorowanie tzw. wiernokątne. Jeżeli wiernie są zachowane kąty, nie mogą zostać wiernie zachowane odległości lub pola powierzchni. Najdokładniejsze odwzorowania zachowują wierność kątów - szczególnie odwzorowania używane przez geodetów. Mapy wojskowe również są wykonane w odwzorowaniach wiernokątnych.
Odwzorowania mało dokładne to odwzorowania kuli. Wykonuje się je dla map w skalach poniżej 1 : 100 000. Mapy dokładniejsze są wykonywane w odwzorowaniach wiernokątnych elipsoidy - bądź wprost na płaszczyznę bądź na pobocznicę walca.
Najczęściej używane odwzorowania to:
- Mercatora (M- Mercator Projection) - odwzorowanie normalne walcowe wiernokątne elipsoidy - walec jest styczny w równiku.
- Uniwersalne poprzeczne Mercatora (UTM - Universal Transwersal Mercator) - odwzorowanie poprzeczne walcowe wiernokątne - walec sieczny do elipsoidy symetralnie do południka osiowego danej strefy.
- Gaussa-Krügera - odwzorowanie walcowe poprzeczne wiernokątne elipsoidy - walec styczny w południku osiowym danej strefy.
- W Polsce obecnie jest używane odwzorowanie płaszczyznowe quasistereograficzne wiernokątne elipsoidy na płaszczyznę (w czterech strefach odwzorowawczych) zwane popularnie odwzorowaniem '65.
W powyższych odwzorowaniach stosowane są następujące formuły [4](tab. 3):
tab. 3
| Obliczenie x,y Ź B,L |
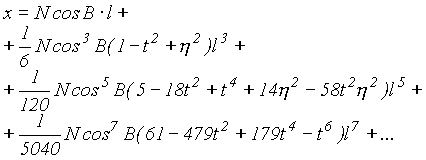
|
przy czym:
S(B)... długość łuku południka
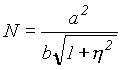 ...promień krzywizny pierwszego wertykału
...promień krzywizny pierwszego wertykału
![]() ...wielkość pomocnicza
...wielkość pomocnicza
![]() ... kwadrat drugiego mimośrodu
... kwadrat drugiego mimośrodu
t = tan B... wielkość pomocnicza
l = l - l0... różnica długości (punktu - południka osiowego)Ú
uważa się powszechnie, że odwzorowania Gaussa - Krügera i Mercatora są oparte o te same zasady matematyczne. Różnice we współrzędnych pochodzą od inaczej przyjmowanego
współczynnika skali:
- w odwzorowaniu Gaussa wiernie odtwarza się południk osiowy; zniekształcenie długości rośnie na zewnątrz, osiągając maksimum na skraju strefy (dla strefy sześciostopniowej zniekształcenie długości wynosi 67 cm na 1 km długości),
- w odwzorowaniu UTM współczynnik skali południka środkowego wynosi 0.9996, na siecznych almukantaratach jest równy 1.0000 i wzrasta w kierunku skraju strefy do 1.0016 (dla pasów sześciostopniowych). W odwzorowaniu UTM zniekształcenia odległości są mniejsze i bardziej równomiernie rozłożone, a zatem powierzchnia elipsoidy jest wierniej odwzorowana na płaszczyźnie niż w odwzorowaniu Gaussa. Współczynnik skali jest prosty w stosowaniu - należy mnożyć przez niego obliczone w odwzorowaniu współrzędne :
y0 = y ? m
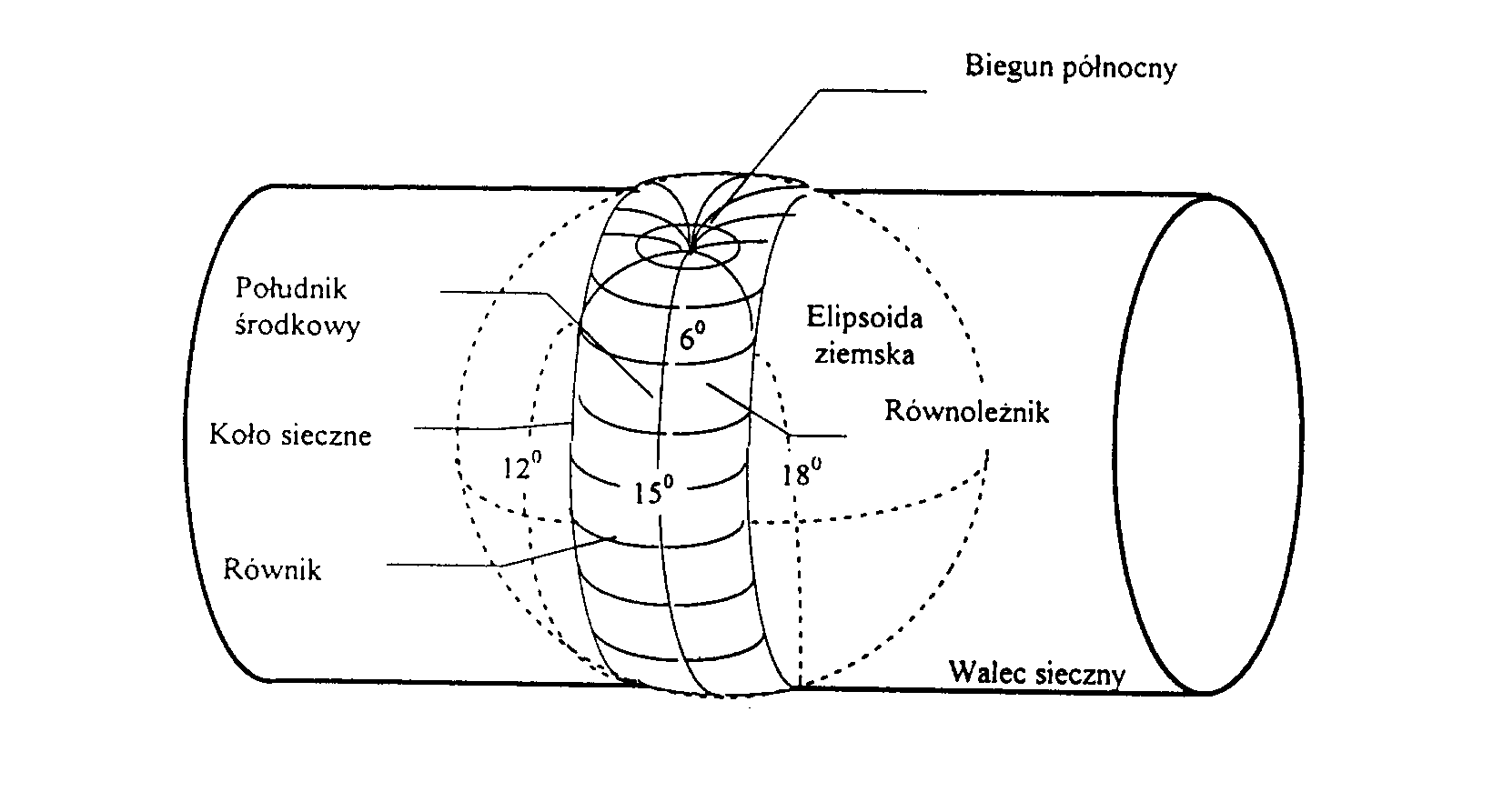
Rys. 3. Ilustracja odwzorowania poprzecznego Mercatora
Przed II Wojną światową w Polsce używane było odwzorowanie Gaussa-Krügera w pasach dwustopniowych . Tworzyły one układy:
1 - poznański o długości geodezyjnej południka osiowego 170,
2 - łęczycki o długości geodezyjnej południka osiowego 190,
3 - warszawski o długości geodezyjnej południka osiowego 210,
4 - lubelski o długości geodezyjnej południka osiowego 230,
5 - wileński o długości geodezyjnej południka osiowego 250.
Powierzchnią odniesienia była elipsoida Bessela styczna do powierzchni geoidy w punkcie Borowa Góra.
Odwzorowanie Gaussa-Krügera do prac kartograficznych stosowane nie było. Władze wojskowe do odwzorowań dla celów wojskowych stosowały odwzorowanie quasistereograficzne Roussilhe'a.
Po II wojnie dla robót geodezyjnych oraz dla opracowania mapy gospodarczej kraju przyjęto odwzorowanie Gaussa-Krügera z podziałem obszaru państwa na pasy trzystopniowe z założeniem, że skala liniowa w każdym południku osiowym wynosiła 0.999935.
Pasy trzystopniowe tworzyły układy:
1 - układ szczeciński o długości geodezyjnej południka osiowego 150,
2 - układ bydgoski o długości geodezyjnej południka osiowego 180,
3 - układ warszawski o długości geodezyjnej południka osiowego 210,
4 - układ białostocki o długości geodezyjnej południka osiowego 240.
Powierzchnią odniesienia jest elipsoida Krasowskiego styczna do powierzchni geoidy w punkcie Pułkowo.
tab. 4
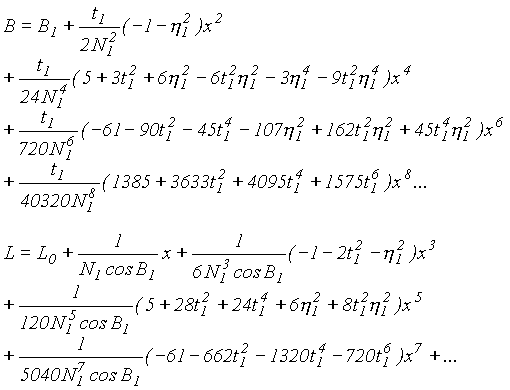 |
gdzie indeks 1 u dołu współrzędnej B odnosi się do umownego punktu o pełnej szerokości geodezyjnej, np. pełnego stopnia. Powyższe wzory są najczęściej realizowane przy pomocy tabel pomocniczych, w których uwzględnione są obliczone długości południków dla pełnych stopni szerokości geodezyjnej, które obejmują terytorium danego kraju (np. dla Polski takie tablice ułożył prof. Hausbrandt lub prof. Gajderowicz). Takie tablice są ułożone zarówno do przeliczania B i L na x i y jak i do zamiany odwrotnej.
Początek układu współrzędnych prostokątnych płaskich x, y pokrywa się z obrazem punktu głównego, a oś x jest skierowana na północ (pokrywa się z obrazem południka osiowego).
Skalę długości w punkcie głównym przyjęto równą 0.999714285. Redukcje długości wynoszą od -20 cm/1 km w okolicy Świnoujścia do +90 cm/1 km w okolicy Leska.
W celu wycofania z użytku w resortach cywilnych współrzędnych układu "42" (odwzorowanie Gaussa-Krügera elipsoidy Krasowskiego) zdecydowano się na wprowadzenie układu, zapewniającego służbom geodezyjnym odpowiednie dokładności - układ nazwano "65".
Za podstawę opracowania przyjęto teorię prof. Lucjana Grabowskiego z Politechniki Lwowskiej.
Wzory, używane w odwzorowaniu [4], przedstawiono w tab. 5.
tab. 5
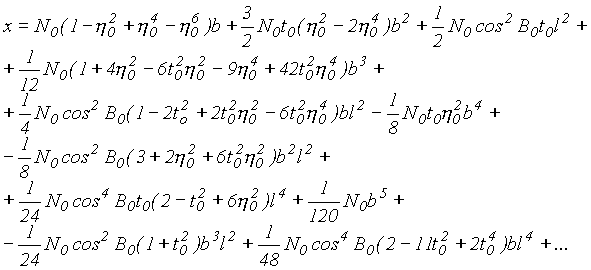 |
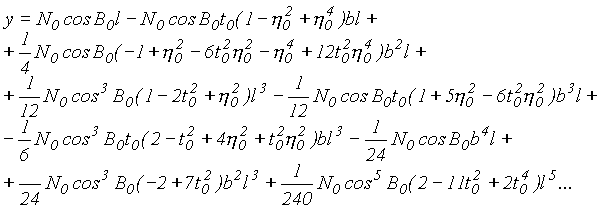 |
przy czym: b i l to różnice współrzędnych elipsoidalnych szukanego punktu oraz punktu głównego danej strefy, N0 i B0 dotyczą również punktu głównego.
Powyższe wzory mogą być przedstawione w postaci wielomianów zawierających szereg współczynników mających na celu ułatwienie obliczeń. Sposób taki przyjęto przy tworzeniu programu "GEOGRAF", przy pomocy którego przeliczane mogą być współrzędne od układu "42" do układu "65". Program ten posiada również procedury pozwalające na obliczenie parametrów transformacji od układu lokalnego do układu "65".
Wzory do obliczenia odwrotnego przedstawiono w tab.6.
tab. 6
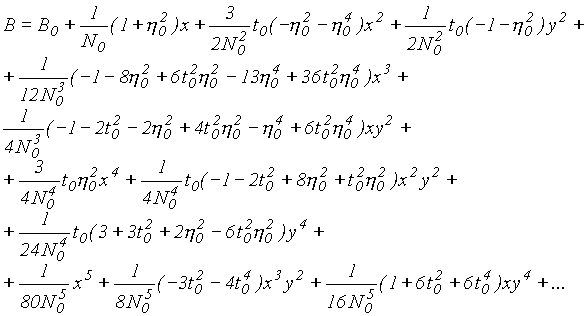 |
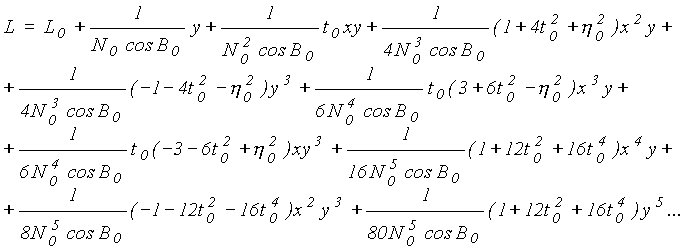 |
przy czym: B0 i L0 to współrzędne punktu głównego danej strefy odwzorowawczej, x, y to współrzędne punktu w układzie "65",
W Polsce mamy 4 układy odwzorowawcze "65", tzw. strefy oznaczone cyframi 1 do5. Wprowadzono je w celu zminimalizowania zniekształceń liniowych. W tabeli 7 przedstawiono zasięgi poszczególnych stref oraz współrzędne punktów głównych każdej strefy.
tab. 7
65/2 65/3 65/4 |
52055' 53030' 51032'30'' |
21030' 17002'30'' 16040' |
51020'- 54030' 52010'- 54050' 49015'- 53020' |
190-24000' 14005'-20000' 14015'-19005' |
5467000 5806000 5999000 5627000 |
4637000 4603000 3501000 3703000 |
W Polsce funkcjonuje jeszcze 5 strefa odwzorowawcza, w której obowiązuje odwzorowanie Gaussa-Krügera. Jest to strefa obejmująca stosunkowo małą powierzchnię - jest to strefa katowicka.
3. Relacje między układami, używanymi w Polsce a globalnym WGS84.
Pomijając wojskowe mapy operacyjne z naniesioną siatką współrzędnych liniowych odniesionych do elipsoidy WGS84 [7], użytkownik systemu GPS staje przed problemem wykorzystania uzyskanych z pomocą odbiorników GPS współrzędnych WGS84.
Wszystkich użytkowników systemu GPS można podzielić na grupy charakteryzujące się różną dokładnością uzyskanych współrzędnych (tab. 9):
tab. 9
II III IV |
1 m 10 m 100 m |
DGPS - tak DGPS - tak Tak |
Topografia DGPS - tak Kod Y Tak |
Po opracowaniu obserwacji Natychmiast Natychmiast Natychmiast |
W zależności od grupy dokładnościowej, w której znajdzie się użytkownik GPS, może być zastosowany mniej lub bardziej dokładny algorytm obliczeniowy.
Zasadą jest, że odbiorniki GPS najczęściej określają swoje współrzędne w postaci B, L, H, przeliczenia natomiast dokonuje się w postaci X, Y, Z. Przeliczenie B, L, H na X, Y, Z jest proste (wzory w tab. 1). W tym obliczeniu musimy używać parametrów elipsoidy WGS84, która jest elipsoidą globalną; dlatego obliczone współrzędne X, Y, Z będą odnosiły się do układu o początku w środku mas Ziemi.
Rozwiązania dla użytkowników 1 grupy dokładności:
Relacja między układem WGS84 a układem "65":
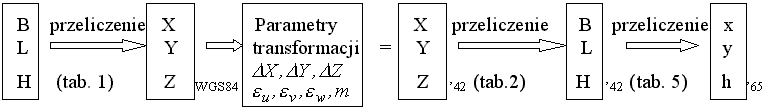
Rys. 4
Na mapach wojskowych w skali 1:50 000 z naniesioną siatka WGS84 podane są przybliżone relacje (dla arkusza mapy z dokładnością do 1m) między współrzędnymi płaskimi (x,y)42 a (x,y)WGS84 [7].
Mapy cywilne w zasadzie (w skalach do 1:50 000) posiadają siatkę współrzędnych x,y w układzie "65". Szereg map ma określone współrzędne narożników w układzie elipsoidalnym "42", siatkę współrzędnych (kilometrową) natomiast we współrzędnych układu "42" w odwzorowaniu Gaussa-Krügera.
Mapy typowo geodezyjne posiadają natomiast tylko siatkę współrzędnych x,y w odwzorowaniu "65".
Relacja między WGS84 a "42"
Dokładną relację opisuje schemat:
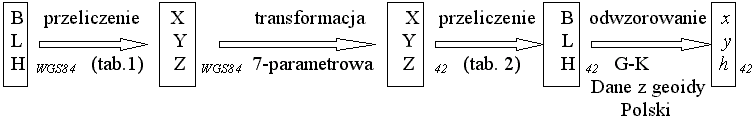
Przybliżoną relację opisuje schemat:
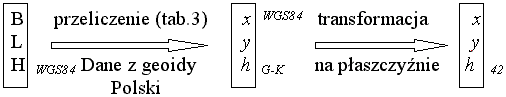
Rys. 5
Schemat pierwszy zapewnia wystarczającą dokładność obliczeń pod warunkiem znajomości dokładnych parametrów transformacji siedmioparametrowej; w przypadku transformacji na płaszczyźnie wyniki nie będą posiadały pełnej dokładności, ponieważ współrzędne płaskie są określane na dwóch różnych płaszczyznach nierównoległych. Dokładność takiej transformacji będzie uzależniona od wielkości obszaru, na którym będą położone wyznaczane punkty.
Pełną dokładność obliczenia współrzędnych (od współrzędnych WGS84 do '65 i h) może zapewnić program TRANSGPS prof. I. Gajderowicza. Program ten oblicza parametry transformacji dla obszaru danej sieci punktów zawierającej punkty łączne, tzn. takie, które posiadają:
1. współrzędne x,y w układzie "65" oraz wysokości w stosowanym układzie wysokości,
2. współrzędne X,Y,Z w układzie satelitarnym WGS84, uzyskane w wyniku wyrównania sieci satelitarnej (dokładność 1 grupy).
W programie TRANSGPS [ 2 ] współrzędne satelitarne X,Y,Z są "przesunięte" o przybliżone wartości DX, D Y, D
Z w celu dopasowania do przybliżonej zgodności układów "42" i "84".
Jednocześnie współrzędne tych samych punktów, znane w układzie "65" oraz ich wysokości są przeliczone na współrzędne B42, L42, H42. Po przeliczeniu współrzędnych X84, Y84, Z84 poprawionych o przesunięcie początku układu na współrzędne B, L, H następuje określenie parametrów transformacji między układami, w których są tak określone współrzędne. Po określeniu wyrównanych parametrów transformacji następuje proces przeliczania współrzędnych wszystkich nowo wyznaczanych punktów na współrzędne w układzie "65" oraz ich wysokości w stosunku do powierzchni odniesienia dla obszaru danej sieci.
Wymienione wyżej procedury korzystają z parametrów transformacji pomiędzy układami. Najprostsza postać transformacji, tzw. 3-parametrowa jest następująca:
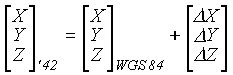
lub na płaszczyźnie - w odwzorowaniu ( 2-parametrowa):
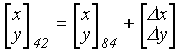
Sposoby określania parametrów transformacji są rozmaite. Mogą one być określone mniej lub bardziej dokładnie. W zależności od typu dokładności użytkownika GPS należy używać parametrów o odpowiedniej dokładności.
Przybliżone parametry transformacji dla obszaru Polski mogą być następujące:
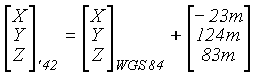
Obliczone w ten sposób przybliżone współrzędne prostokątne należy przeliczyć na elipsoidalne (elipsoida Krasowskiego) a następnie na płaskie w odwzorowaniu Gaussa-Krügera lub "65" w odpowiedniej strefie odwzorowawczej.
Dla porównania zestawiono w tab. 10 dane dotyczące elipsoid odniesienia, używanych w kilku wybranych krajach i ich przybliżonych relacji względem WGS84 [ 1 ]:
tab. 10
1/f = 298.3 |
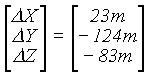 |
||
1/f = 297.00 |
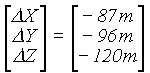 |
||
1/f = 298.3 |
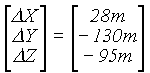 |
||
1/f = 297.00 |
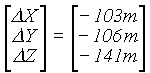 |
Współrzędne WGS84 odnoszą się do układu współrzędnych ziemskich ortokartezjań-skich, realizowanym na bazie zmodyfikowanego układu NSWC 9Z-2 (WGS72 - NNSS TRANSIT).
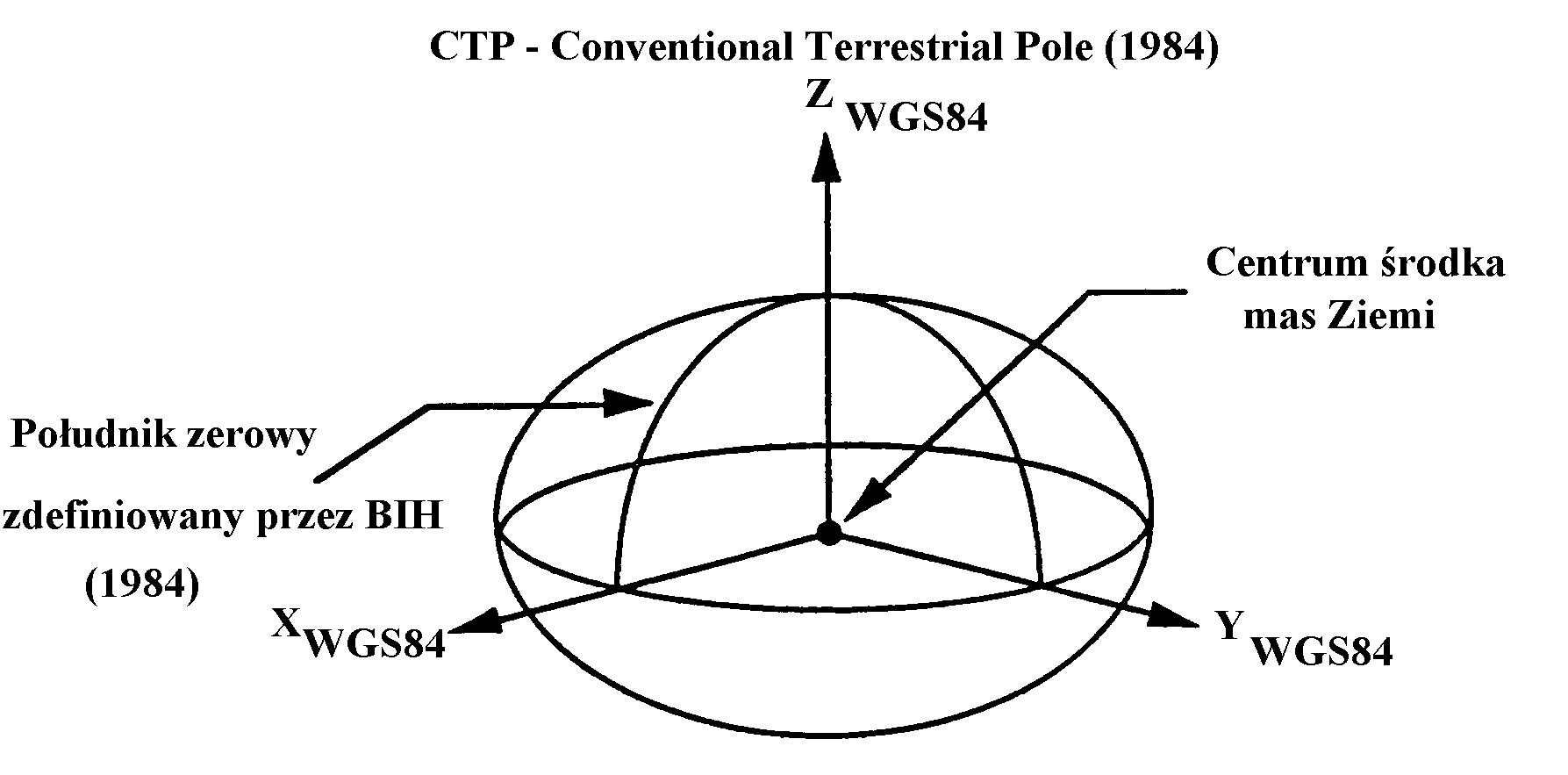
Rys. 6
Początek układu współrzędnych WGS84 (rys. 6 ) pokrywa się ze środkiem mas Ziemi, oś Z jest skierowana do umownego bieguna ziemskiego (Conventional Terrestrial Pole - CTP). Kierunek osi X jest wyznaczony przez przecięcie płaszczyzny południka i płaszczyzny równika związanego z CTP, a oś Y uzupełnia prawoskrętny ortogonalny układ współrzędnych.
Modyfikacje układu NSWC 9Z-2 są następujące:
- przesunięcie początku układu NSWC 9Z-2 o wielkość 4.5 m na południe wzdłuż osi Z,
- obrót południka odniesienia układu NSWC 9Z-2 o kąt 0.814 arc sek wokół osi Z do kierunku zdefiniowanego przez BIH (na początek 1984) jako południk zerowy,
- zmiana skali układu NSWC 9Z-2 o -0.6 ppm.
Transformacja współrzędnych stacji dopplerowskich (WGS72) do układu WGS84 nastąpiła przy zastosowaniu wzorów transformacji Mołodienskiego z użyciem powyższych parametrów.
Początek układu WGS84 jest jednocześnie środkiem geometrycznym elipsoidy WGS84 a oś Z jej osią obrotu.
Matematyczna relacja między ustalonym układem ziemskim WGS84 (Instantaneous Terrestrial System- ITS) a inercjalnym układem odniesienia (Conventional Inertial System - CIS) określona jest zależnością matematyczną:
gdzie:
A = macierz rotacji ruchów Bieguna,
B = czas gwiazdowy,
C = astronomiczna nutacja,
D = astronomiczna precesja.
System CIS jest odniesiony do epoki J2000.0. Wzory służące do przeliczenia współrzędnych z układu WGS72 do układu WGS84 zestawiono w tab.11.
tab. 11
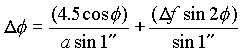 |
|
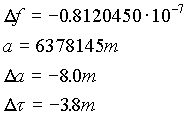 |
|
| Aby otrzymać współrzędne WGS84, należy dodać do współrzędnych WGS72 |
W zastosowaniach geodezyjnych są używane trzy różne powierzchnie:
- naturalna fizyczna powierzchnia ziemi,
- elipsoida odniesienia,
- powierzchnia o jednakowym potencjale, zwana geoidą.
Przy wyborze elipsoidy odniesienia dla systemu WGS84 kierowano się zaleceniami Międzynarodowej Unii Geodezji i Geofizyki, dotyczącymi światowej elipsoidy odniesienia o określonych parametrach (GRS80 - Geodetic Reference System 1980). Dlatego też przyjęto identyczne parametry dla elipsoidy WGS84 co parametry elipsoidy GRS80, z jedną małą zmianą. Dotyczy ona harmoniki zonalnej drugiego rzędu J2. Zdefiniowane parametry elipsoidy WGS84 przedstawiono w tab. 12.
tab. 12
|
Duża półoś Znormalizowana harmonika zonalna drugiego rzędu
Stała grawitacyjna Ziemi (włączając atmosferę w masę Ziemi) Stała grawitacyjna Ziemi (bez udziału atmosfery) Kątowa prędkość obrotu Ziemi (w układzie uwzględniającym ruch precesyjny) |
J2
|
6378137 m
108263×10-8
3986001.5×108m3/s2
(7292115.8553×10-11
|
ą 2 m
ą1.30× 10-9
ą 0.6×108m3/s2 ą 0.1500×10-11rad/s |
gdzie TU - stulecia juliańskie od epoki J2000.0.
Problem określenia wysokości jest odrębnym problemem, wymagającym znajomości odstępów geoidy od elipsoidy WGS84 w danym rejonie [5]. Dokładna mapa takich odstępów zwana mapą geoidy została dla obszaru Polski opracowana w Centrum Badań Kosmicznych PAN przez prof. Adama Łyszkowicza [6].
Posiadając mapę geoidy (w zapisie cyfrowym) można określić odstęp geoidy w dowolnym, o znanych współrzędnych punkcie z dokładnością lepszą od 5 cm. Wówczas:
H = h + N,
lub
h = H - N,
gdzie:
H - wysokość nad elipsoidą WGS84,
H - wysokość określana jako wysokość nad powierzchnią morza.
Na obszarze Polski odstępy elipsoidy satelitarnej WGS84 od geoidy sięgają od 26 m do 43 m.
Literatura:
- [1] Department of Defense World Geodetic System 1984 : Its Definition and Relationships with Local Geodetic Systems. DMA Technical Report 8350.2, The Defense Mapping Agency, 1991.
- [2] GAJDEROWICZ I., Problemy transformowania sieci GPS do układu państwowego "1965". Acta Acad. Agricult. Techn. Olst., 446, Geodaesia et Ruris Regulatio, 23, Olsztyn,
- [3] GAJDEROWICZ I., Kartografia matematyczna dla geodetów, podręcznik, Wydawnictwo ART., Olsztyn, 1991.
- [4] HOFMANN - WELLENHOF B., LICHTENEGGER H., COLLINS J., Global Positioning System : Theory and Practice. Springer - Verlag, Wien - New York, 1994.
- [5] LAMPARSKI J., ŚWIĄTEK K., Wyznaczanie wysokości punktów z wykorzystaniem pomiarów GPS, Zeszyty Naukowe Akademii Rolniczej we Wrocławiu, Geodezja i Urządzenia Rolne XII, Nr. 251, 1994.
- [6] ŁYSZKOWICZ A., The Geoid for the Area of Poland, Artificial Satellites, Planetary Geodesy No 19, Vol. 28 no 2 - 1993
- [7] Wojskowe mapy topograficzne dostosowane do standardów NATO (przewodnik). Sztab Generalny Wojska Polskiego, Warszawa, 1996.